|
Everyone knows that electrical equipments is often specified with a power rating in Watts. Others often see generators specified in VA or Watts (sometimes both) and many people think they are the same thing. They are not, which is why you will sometimes see an item (say a generator or an inverter) specified in Watts and VA and the two figures will be different.
Of course, electricians, electrical and electronic engineers know the difference (or rather should do) but that doesn't really help someone with no electrical technical knowledge answer the question "will this inverter power this load?".
What I intend to do here is explain the difference between the two terms and how it affects this question.
VA is Volts * amps. It is the power that will be dissipated in (or used by) a purely resistive load (say a heating element or light bulb). Watts is volts * amps * PF (power factor). PF is a number between zero and 1. So you can see that Watts will always be less than or equal to VA. Never more.
Real Power is measured in watts.
Apparent Power is measured in VA
There can be a huge difference between the two.
So the question is "what is Power Factor?"
The answer to this lies in two parts as there are two completely different effects that make up Power Factor.
First we will tackle the traditional Power Factor. The one that "old timers" are fully familiar with. That of phase shift.
Let's start with a 50Hz AC supply of 230 volts RMS. This will have a peak voltage of 325 volts. We will feed this 230 volt supply into a load of exactly 100 Ohms. This will result in a current in the load of 230V/100 Ohms = 2.3Amps RMS. Now remember this is AC so the waveforms are changing with respect to time.
Here is the graph. For those not familiar with "oscilloscope" type graphs, the time scale is along the bottom and volts, amps, power etc are on the vertical axes. You can see the AC voltage (in violet) swinging positive up to +325 volts, then negative down to -325 volts, above and below zero volts on the left hand scale.
You can also see the current (in green) swinging positive up to +3.25 Amps, then negative down to -3.25 Amps, above and below zero on the right hand scale.
Notice how the waveform for the current is perfectly aligned along the time axis with the voltage waveform. They are said to be "in phase". They both reach maximum, and minimum and zero at the same time.
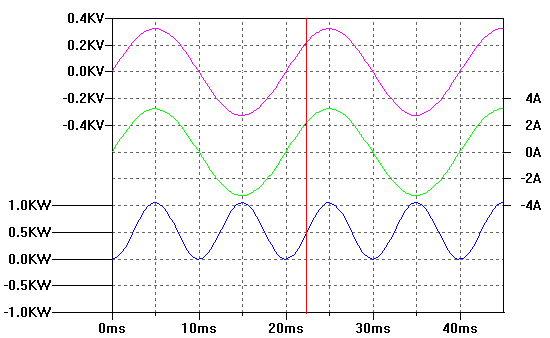
Now look at the trace for the power (in blue). Notice how it starts at zero, when the voltage and current are both at zero. It then rises to its maximum (coinciding with maximum voltage and current) then falls back down to zero (coinciding with the voltage and current both reaching zero).
Then something odd seems to happen. The voltage reverses and becomes negative (starting at 10mS on the time axis) yet the power starts to increase again. This is perfectly correct if you think about it. The voltage reverses (thus becoming negative), but the current also reverses (thus also becoming negative). Power (in watts) is the voltage * current. And a negative multiplied by a negative makes a positive.
To clarify this graph, the power (in blue) is the instantaneous voltage multiplied by the instantaneous current at any single point on the graph. So if we pick a point at say 22.5mS (where the red line is) we can see that the voltage is about 225 volts, the current is at about 2.25 Amps and therefore the power is about 225 * 2.25 = 500 watts which is what the graph shows.
That was all pretty straight forward. That is with a purely resistive load.
Some loads are not purely resistive and this is where it starts to get complicated and this is where Power Factor comes into play.
|
Page last updated 02/04/2008.
Website best viewed on a computer of some sort.